Codex Seraphinianus: Hallucinatory Encyclopedia
by Peter Schwenger
Part of "Cryptotexts": a SCRIPTjr.nl special section.
Preface
The piece that follows was originally presented in 2001 at a British Council symposium on literature and visuality, titled "Seeing Things." That context may explain my play, in the opening paragraphs, with the conference title.
Shortly after the essay was posted on-line, I received an e-mail from one C.O. Jones, who claimed to have decoded the Codex. I followed the link given in the e-mail, to a webpage that failed to convince me of this claim. Both the webpage and C.O. Jones have since then disappeared.
Well, plus ça change, plus c'est la même chose: I see that Kane Faucheris, elsewhere in SCRIPT, once again pursuing the elusive grail of a Codex decoding. In response, I invite Faucher -- and you who are reading this -- to imagine what would be gained by suddenly having in our hands a Codex that was now a full text, probably in Italian. Considerably less weird than the illustrations and our speculations on them, the text would doubtless "explain," in proper encyclopedic fashion, what is now already explained by the illustrations -- or, far more interestingly, what now resists explanation. What we would get from a decoded Codex would be nothing more than the pleasure of "getting it" -- that is, cracking a code. If you are a cryptographer, that pleasure will top all others. But, I would suggest, there is also a pleasure in not getting it. As long as the Codex is not pinned down -- not by Faucher, but also not by me -- it offers itself as an endless source of speculation about its nature vis-à-vis more orthodox encyclopedias, more familiar worlds.
What Faucher refers to as "theoretical flexing" flexes the muscle of the mind. Theory is only another name for thinking -- at its best, that is, when it is not a matter of showing off the range of one's reading and the obscurity of one's terminology. Like anything else, theory deserves to be judged by its best exemplars. I leave it to the reader of the essay that follows to decide which version of theoretical flexing it exemplifies.
This symposium, various no doubt in the approaches taken and examples offered, is gathered under the sign of "Seeing Things." But this unifying sign splits and may be seen in two ways.
First, if we say "he is seeing things," we are understood to be speaking of hallucination --the visual manifestation of unreal entities. To be sure, this definition can apply as well to such things as mental imaging, dreams, and the imaginative participation in fiction.1 We must add, then, another condition: that the one having the hallucination feels, while it endures, that it is real. This helps to distinguish the hallucination from other forms of visualizing, but the scission is not a clean one.2 Hallucination suggests a continuum between vision and visualizing and raises fundamental questions about the ways we distinguish the real from the unreal.
"Behind every real object," Jean Baudrillard asserts, "there is a dream object."3 And at any one time it can never be entirely clear which of these objects we are seeing. So we arrive at the second sense of "seeing things" -- that which reads the word things as referring not to vague entities but to material objects in the world. How do we go about seeing these objects? No matter how broad a range of stimuli is provided by our physical apparatus of seeing, our interpretive reading of those stimuli is necessarily a partial one. We select those features of the object which are felt to be salient or definitive -- and what comes forward as definitive is that which corresponds to an already existing definition. What we see is what we have been prepared to see by systems of classification or categorization.

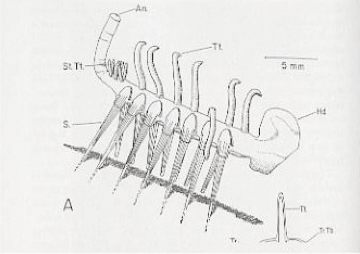 Take this example, a fossilized Cambrian organism excavated in British Columbia (top left).
Take this example, a fossilized Cambrian organism excavated in British Columbia (top left).
Immediately, one tries to sort out this peculiar specimen according to familiar models: one end must be the head, the other the tail or anus; the spikes on one side of the body are defensive and the fragments of legs can be seen protruding underneath. Except that the best reconstruction we have been able to come up with inverts this (bottom left). For the "legs" are actually tentacles, and the defensive spines are struts upon which the creature stands. But these completely unarticulated struts would have been able to propel the organism by only the most minute of increments. And the tentacles, which might be expected to snare food, are too short to carry it to the organism's mouth, at whichever end that might be situated. Since what is designated the head is only an amorphous blob in all the examples found, it may even be that we are dealing here with a fragment of a larger, perhaps stranger, organism. This specimen throws into question all the familiar categories by which we read reality. For this reason, as well as its "bizarre and dream-like appearance,"4 it has aptly been named Hallucigenia.
The categories challenged by this bewildering organism are fundamental to our way of seeing things, or even to the recognition of things as things. Wolfgang-Rainer Mann's recent book, The Discovery of Things,5 claims that Aristotle's early text Categories was not, as some assert, the common sense prolegomenon to his later, more significant work. If Aristotle's text feels like common sense today, that is because the ideas put forth there have become so generally accepted as scarcely to seem like philosophy at all, though they were far from self-evident in their time.
In a radical departure from Plato's doctrine of the Forms, Aristotle asserts that the fundamental entities are ordinary things and their features. As Mann sums it up:
... all the entities need to be divided into particular objects on the one hand, and whatever belongs to those objects on the other (including whatever kinds those objects fall under, in other words, their species and genera). (10-11)
Mann's parenthesis here foregrounds the role of classification in bringing things into definition -- I use the word definition here both in a linguistic-philosophical sense and in the sense of visual focus, for the way we define things determines how we see them. Of the various forms of classification through which things are seen, this essay will focus on the encyclopedia.
Encyclopedias can be broadly divided into two kinds: those that are ordered alphabetically and those that are arranged systematically.
"Alphabetical order" is of course an oxymoron, given the fragmented, arbitrary nature of the alphabet itself. It does provide a quick and convenient way of locating and extracting information, bypassing all that is irrelevant to the item sought. Read in sequence, though, the alphabetical encyclopedia produces only surreal juxtapositions comparable to Raymond Roussel's famous encounter between an umbrella and a sewing-machine upon an operating table -- an image taken straight from the files of hallucination.
The systematic encyclopedia at first seems to do better, to promise an escape from the hallucinatory into a realm of serene order. For instead of an alphabetical jumble, where the only conclusion one could come to would be Robert Louis Stevenson's "The world is so full of a number of things,"6 the systematic encyclopedia provides a philosophical narrative. It presents an ordered view of the universe and the things of this world, as well as of the particular civilization that produced the encyclopedia (and the order of the world picture depicted therein).
If, as in Stéphane Mallarmé's famous pronouncement, the world exists so that it may be put into a book,7 the encyclopedia is an avatar of that book. The encyclopedia that systematizes and classifies, the kind I am addressing, provides its readers with a way of seeing things -- logically and, as a consequence, also visually. Yet this way of seeing things can at times be linked to that other way of seeing things, the hallucinatory. For if psychoanalysis may describe hallucination as "a subjective image which the patient experiences as an external phenomenon,"8 that description applies as well to the fundamental nature of human perception.
Of course our perceptions may be subjected to "reality-testing," and this distinguishes normal perceptions from psychotic hallucinations. Still, this distinction is never entirely secure. What we see depends to a large degree on our ways of seeing. And insofar as the systematic encyclopedia presents us with a categorized way of seeing things, it creates a sense that ordered knowledge is the authoritative reality, while it may be -- must, in a sense, always be -- provisional, incomplete, and to that degree delusory. In this way the classificatory project of the encyclopedia creates an illusion of reality, when it is simply one manifestation among others of "seeing things."
So Michel Foucault, commenting upon the Roussel image already alluded to, reads the "table" upon which the encounter between objects takes place in two ways. The operating table is most obviously another image to be added to those of the umbrella and the sewing-machine. But it is also a classificatory diagram:
A table, a tabula, that enables thought to operate upon the entitles of our world, to put them in order, to divide them in classes, to group them according to names that designate their similarities and their differences.9
And this table operates in a way that may also be described as hallucinatory. Taken to an extreme, whether deliberately or not, classification begins to betray its own claims to a natural order based on the real: "a violent order is a disorder," in Wallace Stevens' words.10 Felt initially to be an accurate reflection of the real, the system at its extreme reveals itself to be arbitrary, unreal. It shares this real-unreal trajectory with the hallucination.
All this can happen unconsciously, when rational systems become oblivious to their own limits: the sleep of reason producing monsters. But there are also deliberately (rather than unintentionally) fictional encyclopedias, such as Borges's encyclopedia of Tlön or his "certain Chinese encyclopedia," quoted by Foucault in the introduction to The Order of Things. These are given to us at one remove, through the reports of their interpreters. However, we have one such encyclopedia that can be held in the hands, experienced directly. It is the Codex Seraphinianus, perpetrated by Luigi Serafini in 1981 and since published in a number of different countries. I cannot say "translated into a number of different languages" since the text is written in a wholly imaginary language, which must remain untranslatable. Imaginary as well is the world depicted in the lavish illustrations -- not just the cities, dress, and customs of beings which are themselves bizarre variations on the human theme, but flora and fauna, and "natural elements" that are utterly foreign to us. While exhibiting at every turn the look of orderly classification, Serafini's encyclopedia is fundamentally hallucinatory, as we shall see. And if this term is a classification, it is also a term -- or rather a state -- that challenges our fundamental notions of classification.
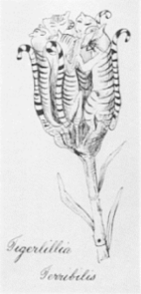
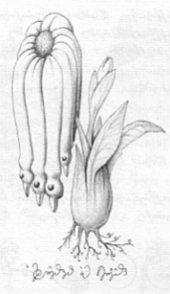
While a few of the book's images have the unclassifiable look of Hallucigenia, the majority are produced by a cross-fertilization between classes. The leading influence seems to be Hieronymus Bosch. Serafini echoes The Garden of Earthly Delights, for instance, in his artificially patterned flora, fantastical architecture, incongruously coupled objects and cryptic rituals. There are also reminiscences of Edward Lear's nonsense botany (top left; Serafini top right). Thus while the sections of this encyclopedia are clearly enough ordered, each section delivers only a systematic disordering. After sections on flora and fauna, the Codex illustrates a genus that consists of pairs of legs, which support not bodies but various surprising terminations such as umbrellas, balls of yarn, striped pods out of which tigers burst when ripe, and numerous free-form shapes.
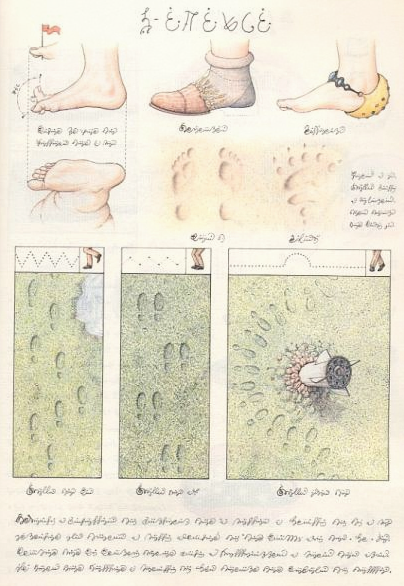
There is a relatively abstract section on natural (or from our point of view unnatural) elements, along with scientific machines for analyzing them. There is a section depicting variations on parts of the human body (bottom left) and one on races, civilizations and customs of the countries shown on a map of the world, a world whose continents and islands seem to have the ability to rearrange themselves at will; there are sections on food, clothing, games, and urban architecture. Perhaps the strangest section is the one on language, where the materiality of the letter is taken to the extreme.
Here letters and words proliferate into different species beyond our own world's superficial differences of language. Forming themselves out of various elements, they flame, drip, and sprout. No longer confined to the plane of the page, they rise above it with the help of gas-filled balloons or are dropped onto it by tiny parachutes. They are literally fished from the mouth or dribbled from it onto a white bib. And under a microscope, the curves of the letters become those of a highway or a stream, populated accordingly, or reveal teeming Dantesque figures.
The language of the Codex Seraphinianus is not as extreme as these; it is inscribed upon the page in the usual fashion. Yet it too foregrounds its material nature, if only because, as a fictional construct, it is opaque to our understanding. There is enough consistency in the labeling of sections and the use of individual characters to foster some hope that this is a cryptogram; but into what known language would these utterly foreign signs be decoded? As the final image of Faucher's gallery illustrates, a sort of Rosetta stone is depicted at the beginning of the language section. However, it provides no illumination, pairing the language of the Codex with a more archaic, and equally fantastical, hieroglyphic system.
It is not a matter, then, of either decoding or translating. Rather, the text of the Codex is an example of what I am calling "glyptolalia", a common technique used by book artists.11 The word is formed by analogy with oral glossolalia, the phenomenon of "speaking in strange tongues" -- but it refers to the inscription of imaginary languages in a text, where it is the glyph (sign, character) rather than the glossé (tongue) that babbles ("lalein"). Despite this distinction, it will be useful for us to remind ourselves here of some of the things that Michel de Certeau has said about glossolalia.
A "vocal utopia," he calls it, explaining his phrase as follows: "what utopia is to social space, glossolalia is to oral communication; it encloses in a linguistic simulacrum all that is not language and comes from the speaking voice."12 De Certeau is using the term utopia in accordance with its etymological sense of "not-a-place" and is drawing a trajectory to the not-a-language that is glossolalia --which nevertheless creates an illusion of language, an abstract language cut loose from the necessity to mean. Similarly, glyptolalia is not-a-writing that becomes the abstract material manifestation of writing per se. As with glossolalia, it simultaneously invites and withstands attempts at interpretation; thus its relation to meaning is, as de Certeau has it, "in the mode of equivocation" (36; Certeau's emphasis).
To assert that the text of the Codex Seraphinianus is equivocal is also to say this of the things depicted therein, the ordered images of a utopia, of a not-place. The text of an ordinary encyclopedia is intended to explicate the things that have been ordered into a system, and while doing so to remove any equivocation in the illustrations through an interpretive commentary; that is what the text contributes to the overall encyclopedic project of "seeing things." This seeing, however, is accomplished by a selective blindness, a focus attained by filtering out. The encyclopedia is already selective in the things that it has chosen to be worthy of seeing; it becomes more so in the ways it chooses to represent visually phenomena that are always more complex than their depiction on the page. But the final act of seeing performed by the encyclopedia is its text.
When scientific classification took shape in the seventeenth century, it was through deliberately limiting the range of perception. As Foucault puts it, in The Order of Things, "Observation, from the seventeenth century onward, is a perceptible knowledge furnished with a series of systematically negative conditions" (132), conditions which excluded certain sense data as too amorphous to be reliable. Vision is considered the most trustworthy mode of perception, but even here what one is allowed to see is what lends itself to ordered description. That description is of the order of language more than the visual order of things:
By limiting and filtering the visible, structure enables it to be transcribed into language. It permits the visibility of the animal or plant to pass over in its entirety into the discourse that receives it. (Foucault 135)
The grammatical structures of language, then, are related to the systematic encyclopedia's broader structures of classification. The tendency to accept both as authoritative and even natural is pulled up short by the glyptolalic text. There language is no longer a transparent means of access to knowledge, but obtrudes itself in a dense and baffling materiality. It is just ordered enough to promise the component of meaning that is associated with language -- but that promise is not fulfilled. We are left in the realm of equivocation, both in regard to language and to the broader systematizing project of which it is such an important part.

As an encyclopedia, fictional though it may be, the Codex Seraphinianus is devoted to the classificatory way of "seeing things." But its text and its illustrations alike, hovering uneasily between a recognizable real and a baffling unreal, partake as well in that other sense of "seeing things" with which I have dealt here: hallucination. To name things and to classify them are ways of bringing them into focus, both visually and as objects of knowledge; but the Codex brings into focus naming and classifications themselves, and implicitly reveals their systems of order to be hallucinatory. If an hallucination is a visual manifestation of unreal entities, the Codex Seraphinianus is such a manifestation, designed precisely to reveal the unreality of the encyclopedic project.
Thus the very last page of the Codex (left) -- after what is either a table of contents in the French manner or an index -- appears to be a kind of afterword. Except that the words on the page are as incomprehensible as ever, their explanation lost to us along with the author who feels the need for one last explanation, an explanation whose subject this time is the entirety of the work just completed. If we cannot decipher the words, though, we can find a kind of message in their material chirography.
For the first time, on this last page, the Codex' text -- whose letters have been so tidy, orderly, and consistent as almost to seem a type font -- betrays that it has been written by a human hand: there are revisions of the text, with words crossed out at certain places and inserts added at others. And as we move down the depicted page, it reveals itself as a depiction by apparently scrolling under itself (upon the actual page, which of course does no such thing). We see that the page has also served as a wall, one of four that form a narrow, high, blank enclosure. On the floor of this cell are the bones of what appears to have been a hand, a ring that may have adorned one of its fingers, a pile of dust drifted into a corner. If this is a cell, it is only big enough to have contained that hand: a metonym of the handiwork on the page above it and throughout the encyclopedia as a whole.
But wholeness is exactly what is thrown into question here -- by the necessity for an afterword, akin to the Derridean supplement; by the chirographic fissures in the text, which thus reveals itself to be not authoritative product but process; by the fact that that process is interminable, as represented here by the text that does not conclude but curls under itself, still babbling as it disappears; by the fact that there is nothing that could be interpreted as equivalent to the graphic sign The End or Fin except the depiction of a material memento mori. All this adds up to a reversal of the encyclopedic project of wholeness, order, and control: the page furls back to reveal the fundamental futility of that project, and of its claims to a comprehensive ordering of the real.  The only signs of life in this decor of death, this crypt that underlies the cryptic, are some tiny rainbow-striped creatures who nestle in the dust or bounce impudently across the floor. Of course one wants to identify these, and what could be more natural in such a case than to turn to the encyclopedia? In the world of the Codex Seraphinianus they are most likely to belong to the lowest levels of the fauna -- specifically to a species of creatures who live, apparently, within a serpentine band of greenery that writhes across the sky (left).
The only signs of life in this decor of death, this crypt that underlies the cryptic, are some tiny rainbow-striped creatures who nestle in the dust or bounce impudently across the floor. Of course one wants to identify these, and what could be more natural in such a case than to turn to the encyclopedia? In the world of the Codex Seraphinianus they are most likely to belong to the lowest levels of the fauna -- specifically to a species of creatures who live, apparently, within a serpentine band of greenery that writhes across the sky (left).
Yet among the various forms depicted on this page of the encyclopedia we cannot find the specific creatures we seek; and we are baffled to think how such creatures of the air could have come to inhabit that close and airless cell. In this way, once again, the encyclopedia's comprehensive project is revealed to be delusory. Meanwhile the sprightly, bouncing, luridly colored mites remind us of a hallucinatory life that has nothing to do with failed human projects.
The disturbing implication of this last page, and of every page of the Codex Seraphinianus, is that the real as we see it cannot contain everything. Other possibilities are continually generated by the imagination , and generated above all in images. Perhaps it is not as important as we thought to determine whether the images generated are those of the artist, the dreamer, the fantasist or the hallucinator; for these species belong to one genus. The images we allow ourselves to see, whether in the mind's eye or in the world, are a small subset of the teeming matrix of possibilities.13 Everything seen outside of the categories by which we allow ourselves to see the real is categorized in turn as a merely seeming reality -- that is, as hallucination. But a book like the Codex Seraphinianus reminds us that categories themselves, with their claims to reflect the real, may be the most delusory hallucination of all.
Editor's Note
Earlier versions of this essay appear here: http://web.me.com/pschwenger/Site/Codex_Essay.html (13 December 2010. "Codex Seraphinianus, Hallucinatory Encyclopedia," Peter Schwenger homepage, n.d.) and in Schwenger's monograph The Tears of Things: Melancholy and Physical Objects (U of Minnesota P, 2006).
- See my Fantasm and Fiction: On Textual Envisioning (Stanford UP, 1999). Incidentally, the original title of this book was to be Hallucinated Pages; the concept of the fantasm prevailed because it covered a broader range of visualizations. ↩
- See C. Wade Savage, "The Continuity of Perceptual and Cognitive Experiences" (In Hallucinations: Behavior, Experience, and Theory. Ed. R.K. Siegel and L.J. West [John Wiley and Sons, 1975]), 257-286. ↩
- Jean Baudrillard, The System of Objects (Trans. James Benedict [Verso, 1996]), 117. ↩
- Stephen J. Gould, Wonderful Life: The Burgess Shale and the Nature of History (Norton, 1989), 154. Information on Hallucigenia is taken from pages 153-57 of this work. ↩
- Wolfgang-Rainer Mann, The Discovery of Things: Aristotle's Categories and Their Context (Princeton UP, 2000). ↩
- Robert Louis Stevenson, "Happy Thought," A Child's Garden of Verses and Underwoods (Current Literature Publishing Co., 1906). A copy of Stevenson's collection is readily available online, at Bartleby.com (May 2000), for example: http://www.bartleby.com/188/index2.html (13 December 2010). ↩
- Stéphane Mallarmé, "The Book, Spiritual Instrument" (In Selected Poetry and Prose. Ed. Mary Ann Caws. New Directions, 1982), 80. The original French, according to Wikiquote ("Stéphane Mallarmé," 25 November 2010. http://en.wikiquote.org/wiki/St%C3%A9phane_Mallarm%C3%A9 [13 December 2010]) reads, "Le monde est fait pour aboutir à un beau livre." ↩
- Charles Rycroft, A Critical Dictionary of Psychoanalysis (Thomas Nelson, 1968), 60. ↩
- Michel Foucault, The Order of Things: An Archaeology of the Human Sciences (Vintage, 1994), xvii. ↩
- Wallace Stevens, "Connoisseur of Chaos" (In Collected Poetry and Prose. Library of America, 1997), 194. ↩
- Other examples include Jan Sawka, A Book of Fiction (Clarkson N. Potter, 1986) and Timothy Ely, The Flight into Egypt (Chronicle, 1995). An interview with Ely, and examples of his work, appear in this special section: https://scriptjr.nl/special-sections/cryptotexts/timothy-ely (13 December 2010. Timothy Ely, Interview. SCRIPTjr.nl 2.1, January 2010). ↩
- Michel de Certeau, "Vocal Utopias: Glossolalia" (Representations 56 [Autumn 1996]: 31). ↩
- That fertile matrix in the mind's eye may sometimes be glimpsed, I would suggest, in the phenomenon of hypnagogia. I have analyzed that phenomenon in relation to visualization by readers in Fantasm and Fiction, 37-40. See also Andreas Mavromatis, Hypnagogia: The Unique State of Consciousness between Wakefulness and Sleep (Routledge, 1991). ↩







 SCRIPTjr.nl
SCRIPTjr.nl